Deconvolution Module

The deconvolution modules helps to create a spectral function which is applied during reconstruction process to all data together with the spectra of the filtering moduls. To do convolution processing a individual reference signal is necessary. A reference signal from the library can be selected by “File -> load filer from bank”. You can generate a reference signal by yourself with “Tools -> Call extract reference module”

This module provides the implementation of the following signal processing techniques.

1. Filtering

2. Correlation

3. Convolution

4. Deconvolution

5. Phase deconvolution

Wherein every process can be adapted to use following window functions as filterfunction in frequency domain

1. tapered Cosine Window

2. Bartlett Hann Window

3. Bartlett Window

4. Blackman Window

5. Chebyshev Window

6. Gaussian Window

7. Hamming Window

8. Hann Window

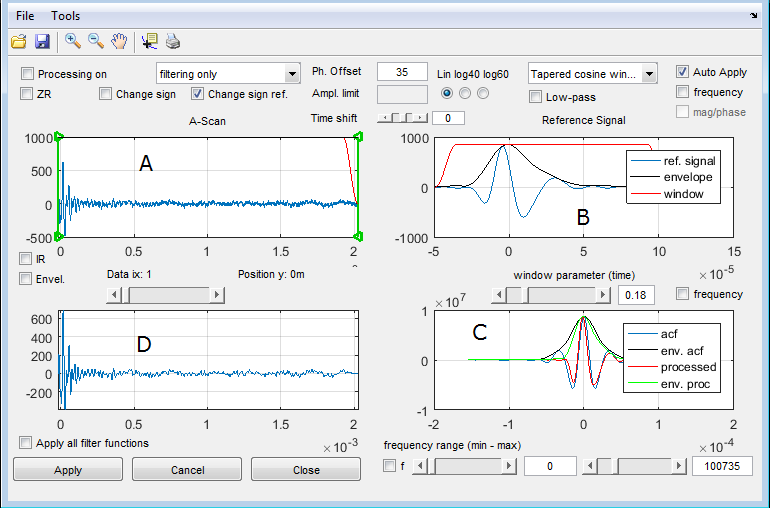
The visualization of output contains 4 subplots. (A) One selected A-scan, (B) Used reference signal + Filter, (C) Processed A-scan, (D) Processing results on reference signal.

Common Parameters

Parameter	Meaning
Filtering on	Switch for applying filtering to the data
2. Process Level	Select a second filter setting for the second reconstruction step (usually unused!)
ZR	Zoom Reset
IR	Impulse Response: Apply the filter operation to a synthetic Dirac impulse
Envel.	Display additionally the envelope of the processed signal in “D”
Change sign	Change the sign of the processed signal
Change sign ref.	Change the sign of the used reference signal. Filtering uses no reference signal
Ph.Offset	Phase offset multiplied as complex number \(\exp (j \phi )\) on each frequency value.
Ampl. limit	Parameter used only for deconvolution
Time shift	Additional time delay multiplied as complex number \(\exp(j \omega t_0)\) on each frequency value
Lin log40..	Linear or logarithmic display of spectrum
Filter parameter	Filter parameter for the tukey filter function in frequ. domain 0: rectangle 1: 1-cosine
Low-pass	Switch from band-pass to low-pass type of filterfunction
frequency	display plot of frequency and filterfunction of data or time domain and window function of reference
freq. range	definition of the minimum and maximum frequency of the bandpass filter function
Auto Apply	If set, changes of parameter are immediately applied to the data and a recalculation of the reconstruction is induced.

Filtering

The deconvolution module can be used like the filtering 1 module. There are 2 features which are only available here:

• additional phase offset applied to all spectral values

• additional time shift applied to all A-scans

Convolution, Correlation

Convolution and correlation techniques require a reference signal, which must be sampled with the same frequency like the data itself. The method is strait forward, additional filtering, phase offset and time delay may be applied.

Deconvolution, phase deconvolution

Deconvolution by a reference signal means that, the signal is divided by the spectrum of a reference signal. Spektral division results in big problems if the reference signal itself is not noise free or contains frequency values with low amplitude. We use a Wiener Filtering approach, where an extra parameter in the denomintor can manually applied as Ampl.limit which is a value normalised to the maximum of the spectrum. The resulting filter function is plotted in B, so that you may observe the effect. Usually an additional filter function has to be applied to get a useful impulse response. The effect of the processing can be observed in plot “C”. This plot can be magnified by the pressing the right mouse in plot “C” and selecting “Plot in extra figure”.

To avoid the problems with deconvolution and the division by small noisy frequency you may selelect the option “phase deconvolution”. This means that the original spectral energie of the signal is preserved and only the phase of the signal is compensated. This technique works very well if the reference signal does not contain multiples of an impulse.

Example: Parameters for filtering

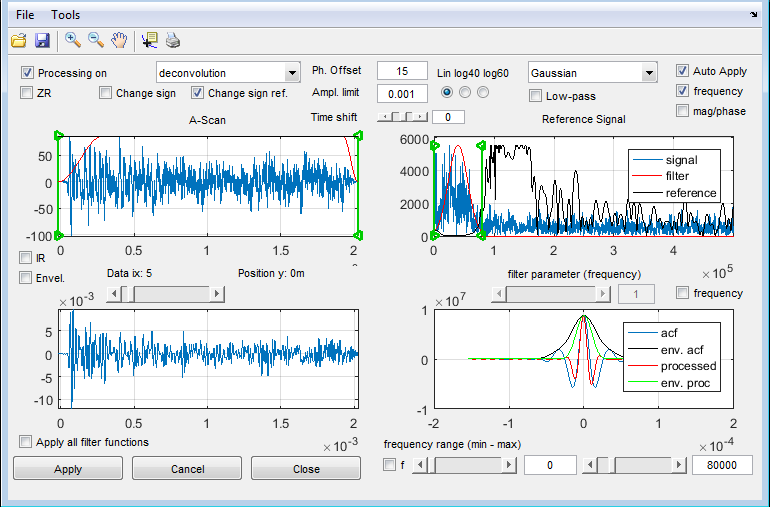
Example: Parameters for deconvolution

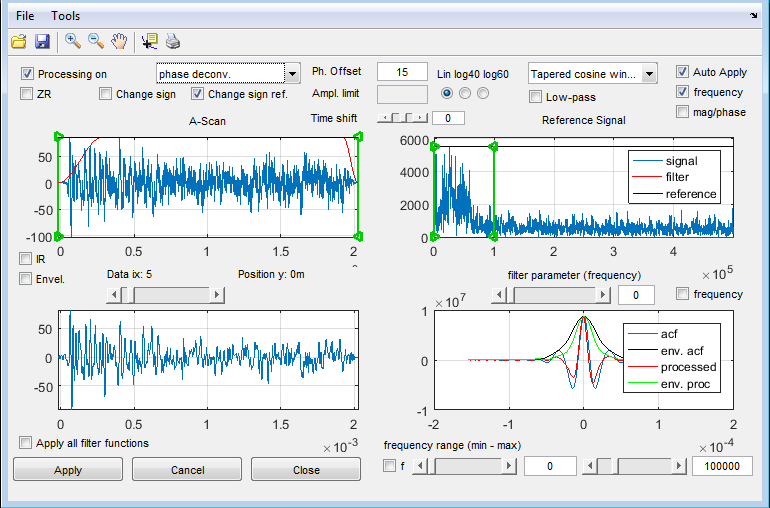
Example: Parameters for deconvolution

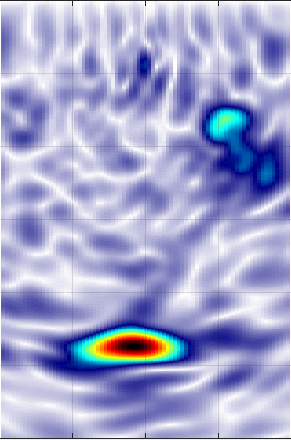
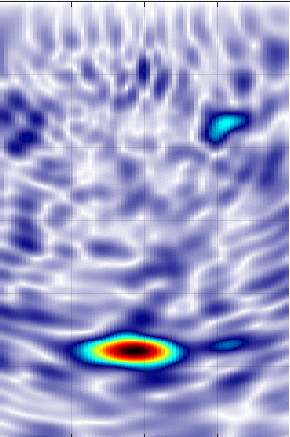
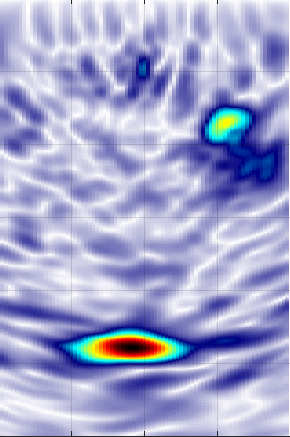
Example of a SAFT envelope image of an ultrasonic reflection from a tendon duct and a backwall. Left: filtering, middle: deconvolution, right, phase deconvolution

Note

The phase offset is important

1. if you want to compare phase values in the reconstruction

2. if you want to do a very precise depth estimation by evaluating the real part of the reconstruction.

Remember: The reference signal is gained from a signal in a specific depth (e.g. backwall at 300mm). In the case of superpositions of small single transducer signals the phase of the complete signal is depth dependend.